How many sig figs in 0.010 – How many significant figures in 0.010? Embark on a journey to unravel this intriguing numerical enigma. Significant figures, the cornerstone of scientific measurements, hold the key to unlocking the secrets of precise calculations and accurate data analysis.

Delve into the fascinating world of significant figures, where the presence or absence of zeros plays a pivotal role. Discover how trailing zeros can make all the difference, and explore the transformative power of scientific notation in representing numbers with varying levels of precision.

Significant Figures in 0.010

In scientific measurements, significant figures are the digits that are known with certainty and the first uncertain digit. They play a crucial role in accurately reporting and interpreting experimental data.

The number 0.010 has 2 significant figures. If you’re looking for a detailed study guide for Act 3 of Macbeth, you can check out this act 3 macbeth study guide . Coming back to our topic, the number 0.010 has 2 significant figures because the zeros in front of the 1 are not significant.

Determining Significant Figures, How many sig figs in 0.010

To determine the number of significant figures in a number, follow these rules:

1. Non-zero digits are always significant.
2. Zeros between non-zero digits are significant.
3. Leading zeros (zeros before the first non-zero digit) are not significant.
4. Trailing zeros (zeros after the decimal point and after all non-zero digits) are significant only if the number is written in scientific notation.

In the case of 0.010, there are two significant figures: 1 and 0.

Trailing Zeros and Significant Figures

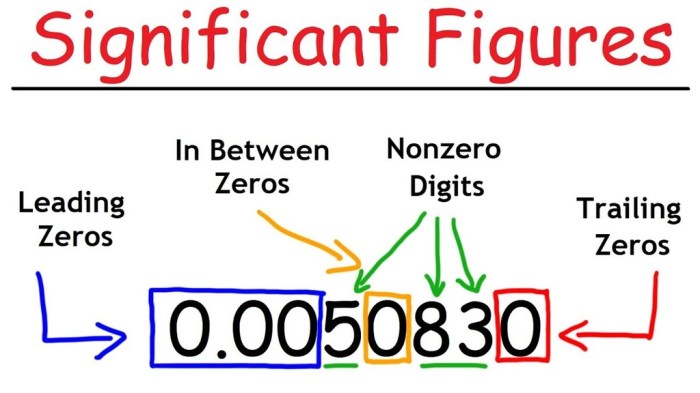
In determining significant figures, trailing zeros play a crucial role. Trailing zeros after a decimal point are significant, indicating the precision of the measurement. Conversely, trailing zeros before a decimal point are not significant and serve only as placeholders.

Zeros After a Decimal Point

• Example: 0.010 has two significant figures because the trailing zero after the decimal point indicates the precision of the measurement.

Zeros Before a Decimal Point

• Example: 100 has only one significant figure because the trailing zeros before the decimal point are not significant and merely serve as placeholders.

Scientific Notation and Significant Figures: How Many Sig Figs In 0.010

Scientific notation is a way of representing numbers in a more compact form, especially when dealing with very large or very small numbers. It is also useful for representing numbers with varying numbers of significant figures.

Converting Numbers to Scientific Notation

To convert a number to scientific notation, follow these steps:

1. Move the decimal point to the right or left until there is only one non-zero digit to the left of the decimal point.
2. Count the number of places you moved the decimal point.
3. Multiply the number by 10 raised to the power of the number of places you moved the decimal point. The exponent will be positive if you moved the decimal point to the left and negative if you moved it to the right.

Converting Numbers from Scientific Notation

To convert a number from scientific notation, follow these steps:

1. Multiply the number by 10 raised to the power of the exponent.
2. Move the decimal point to the right if the exponent is positive and to the left if the exponent is negative.

Significant Figures in Scientific Notation

When converting a number to scientific notation, the number of significant figures remains the same. For example, the number 0.010 has two significant figures, and when it is converted to scientific notation (1.0 x 10^-2), it still has two significant figures.

Applications of Significant Figures

Significant figures are essential in scientific fields as they ensure accurate calculations and data analysis. They provide a consistent method for expressing the precision of measurements, helping scientists draw meaningful conclusions from their experiments and observations.

Applications in Chemistry

• In titrations, significant figures determine the accuracy of the calculated concentration of a solution.
• When calculating the molar mass of a compound from its elemental analysis, significant figures ensure the precision of the result.

Applications in Physics

• In measuring the velocity of an object, significant figures determine the accuracy of the calculated acceleration or displacement.
• When calculating the force acting on an object, significant figures ensure the precision of the result.

Applications in Biology

• In measuring the concentration of a DNA sample, significant figures determine the accuracy of the calculated number of DNA molecules.
• When calculating the growth rate of a bacterial population, significant figures ensure the precision of the result.

Key Questions Answered

Q: Why are significant figures important?

A: Significant figures provide a measure of the reliability of a measurement, ensuring accurate calculations and data analysis.

Q: How do trailing zeros affect significant figures?

A: Trailing zeros after a decimal point are significant, while trailing zeros before a decimal point are not.

Q: Can scientific notation be used to represent numbers with varying significant figures?

A: Yes, scientific notation allows us to express numbers with different levels of precision, preserving significant figures.